|
二、初中数与代数课程内容的特点
(一)初中数与代数课程的价值取向及课程内容的基本结构
1.价值取向
作为义务教育阶段最基本、最主要的课程内容之一,初中阶段的数与代数课程内容,对于发展学生的数感、符号感和抽象思维,促进学生在数学上的全面发展,具有其它内容不可替代的作用;同时,数与代数的思想与方法对于学生理解数学的意义、进而发展问题解决的能力以及形成正确、完整的数学观具有十分重要的作用。
2.内容特点
初中“数与代数”的内容主要包括数与式、方程与不等式、函数,它们都是研究数量关系和变化规律的数学模型,可以帮助人们从数量关系的角度更准确、清晰地认识、描述和把握现实世界。
就具体内容而言,初中数与代数涉及实数、整式和分式、方程和方程组、不等式和不等式组、函数等知识,数、形及实际问题中蕴涵的关系和规律的探索,一些有效地表示、处理和交流数量关系以及变化规律的工具等内容。期望通过学习,发展学生的符号感,体会数学与现实生活的紧密联系,增强应用意识,提高运用代数知识与方法解决问题的能力。
(二)初中数与代数课程内容的主要特点
数与代数领域的内容包括数与式、方程与不等式和函数,它们都是研究现实世界数量关系和运动、变化规律的数学模型。
1.重视数字的现实意义以及对数字的感受,体会数字用来表示和交流的作用。
通过探索丰富的问题情景发展代数运算的意义,在保持基本笔算训练的前提下,强调能够根据题目条件寻求合理、简捷的运算途径和运算方法,加强估算,引进计算器,鼓励算法多样化;淡化繁杂的数字计算(如淡化二次根式的运算),适当弱化恒等变形(如多项式计算,乘法公式,因式分解),适当削弱二次函数的极值问题,无理方程、可化为一元二次方程的分式方程等内容不作要求。
应当看到,寻找问题的精确解是重要的,寻找具有某一精确度的近似解也同样是重要的。基于这一认识,“数与代数”重视寻求具有某一精确度的近似解,强调估算的重要性。通过估算和求近似解,使学生形成和发展数的意识,特别是获得对大数和小数的感受;同时也十分强调用图解法求代数问题的近似解。例如,一次水灾大约有20万人的生活受到影响,灾情将持续一个月。请推算:大约需要准备多少顶帐篷?多少吨粮食?(假如平均一个家庭有4口人,那么20万人需要5万顶帐篷;假如一个人平均一天需要0.5千克的粮食,那么一天需要10万千克的粮食……)
2.通过探索丰富的问题情景,通过数学活动、数学实验,使学生获得数感、符号感,体会数字和符号用来进行表示及交流的作用,并感受数学与现实世界、数学与自然和人类社会的密切联系。
对于应用问题,强调现实性、趣味性和可探索性,题材呈现形式多样化(表格、图形、漫画、对话、文字等);强调对信息材料的选择与判断(信息多余、信息不足……);解决问题策略多样化,问题答案可以不唯一;淡化人为编制的应用题类型及其解题分析。例如,结合自己的生活经验,对代数式3a+1作出解释。学生可以这样说,用100元买了价格相同的三个茶杯,剩1元钱,每个茶杯的价格是a元,那么,3a+1可以解释为:这是三个价格相同的茶杯的总价格与1元钱的和,它等于100元…。
3.突出代数的思维特征,强化符号表示极其转换。
《课程标准》认为,数学对象的多重表示及表示之间的转换,是“数与代数”学习的核心,通过问题的符号表示、表格表示、图像表示和语言表示,使学生初步体会数学可以发现、描述、分析客观世界中多种多样的模式,从多个角度获得对数学概念和数学过程的感受和认识,把握事物的变化和事物间的关系,初步发展学生的符号意识,学会用符号表达现实问题中的一些基本关系,会初步进行符号运算。例如,用图形计算器(或其他辅助手段),探索二次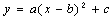 的参数 的参数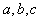 的变化对图像的影响,以及图像变化对参数 的变化对图像的影响,以及图像变化对参数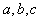 的影响。 的影响。
4.《课程标准》下的“数与代数”强调选择实际性、趣味性、探索性强的应用问题,强调对信息材料的选择和判断,强调解决问题策略的多样化,强调实际问题数学化的过程,强调培养和发展学生的数学应用意识及数学应用能力,使学生初步体会数学可以帮助人们发现、描述、分析客观世界中多种多样的模式,把握事物的变化和事物间的关系。
在《课程标准》下,方程和函数是刻画现实世界,有效地表示、处理、交流和传递信息的强有力工具,是探究事物发展规律,预测事物发展的重要手段。《课程标准》重视对简单现实问题的建模过程,主张让学生学会选择有效的符号运算程序和方法解决问题,重视近似解法特别是图像解法。
5.《课程标准》把现代技术手段(计算机、计算器)的运用作为教与学必不可少的辅助手段,并认为现代技术的运用不仅改变教数学、学数学、用数学的方式,还必将引起对学校数学的重新认识,引起课程观、教学观等深层次的变化。
事实上,《课程标准》对计算器、计算机的基本定位是,帮助学生从繁杂的计算中挣脱出来、解放出来,使得学生有更多的时间和精力投入到具有探索性和挑战性的问题研究之中。例如,用计算器探索开平方的规律----任意在计算器上输入一个不等于0且大于1的正数,如2,连续不断地进行开平方运算,观察所得的结果有什么规律?你能解释其中的道理吗?
如果更换为其它的不等于0且大于1的数,是否也有类似的规律?
如果更换为其它的不等于0且小于1的正数,是否也有类似的规律?
(屏幕上显示的结果呈现这样的规律----如果输入的数字a是大于1的数,那么,屏幕上显示的数值逐渐减小,越来越接近于1,但不等于1,当超过计算器的精确度时,屏幕上显示出1;如果输入的数字a是小于1的正数,那么,屏幕上显示的数值逐渐增大,越来越接近于1,但不等于1,当超过计算器的精确度时,屏幕上显示出1;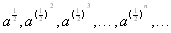 表示屏幕上显示的结果,随着开方次数n的增加, 表示屏幕上显示的结果,随着开方次数n的增加,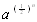 的指数在不断减少,其值视a小于1(大于1)而不断增加(减少),但当开方次数n充分大时, 的指数在不断减少,其值视a小于1(大于1)而不断增加(减少),但当开方次数n充分大时,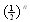 充分小,越来越接近0, 充分小,越来越接近0,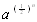 的值也越来越接近1) 的值也越来越接近1)
6.强调代数推理
《课程标准》认为,推理与证明是重要的数学内容之一,通过“数与代数”的学习,使学生得到推理与证明的训练,并逐步理解数学思维的特点、体会证明的意义。这是《课程标准》“数与代数”区别于《教学大纲》“代数”的又一特点。例如:
下表是某月的月历:讨论如下问题:
| 一 |
二 |
三 |
四 |
五 |
六 |
七 |
| |
|
|
1 |
2 |
3 |
4 |
| 5 |
6 |
7 |
8 |
9 |
10 |
11 |
| 12 |
13 |
14 |
15 |
16 |
17 |
18 |
| 19 |
20 |
21 |
22 |
23 |
24 |
25 |
| 26 |
27 |
28 |
29 |
30 |
|
|
你能从日历中发现有趣的结论吗?
让我们来观察阴影部分的四个数,你注意到这四个数的特点了吗?你是否比较了对角线上两个数的乘积?
如果对角线上两个数的乘积分别是65和72,那末这四个数分别是多少?
试找出适合所有这样四个数的规律。你认为这个规律适合任意一个月吗?证明你的结论。
如果在表中任选3行、3列的9个数,你能发现其中的某些规律吗(如,这9个数的和有什么规律)?(如,最后一个问题的参考答案是:如方框中9个数的和是144,如果我们用a表示方框中间的数,则方框中的数可以表示为图示中的关系。很显然,这9个数的和等于9a。因此我们判断任意一个这样方框中的9个数的和都是中间数的9倍。而且,该规律适用于任意一个月的日历。)
| a-8 |
a-7 |
a-6 |
| a-1 |
a |
a+1 |
| a+6 |
a+7 |
a+8 |
7.强调代数的表达与交流功能
代数是一种语言,是表示与交流的手段。既然是一种语言,代数不可避免地就要有它的语法规则。同时代数也是一种问题解决的工具。既然是一种工具,学生不可避免地就要经历语法操练——形式演算的过程,以达到运用代数这一工具进行问题解决的目的。但是《数与代数》认为应通过探索丰富的问题情境理解运算的含义,在保持基本笔算训练的前提下,能够根据题目条件寻求合理、简捷的运算途径和运算方法,强烈主张淡化繁杂的数与式的计算、淡化恒等变形,并把带分数运算、根式计算、无理方程列为基本要求之外。
|