|
二、高中数学典型内容分析1-算法初步
算法是数学及其应用的重要组成部分,是计算科学的重要基础。随着现代信息技术飞速发展,算法在科学技术、社会发展中发挥着越来越大的作用,并日益融入社会生活的许多方面,算法思想已经成为现代人应具备的一种数学素养。需要特别指出的是,中国古代数学中蕴涵了丰富的算法思想。
算法初步是高中数学《课程标准》课程内容的一个模块。在本模块中,学生将在义务教育阶段初步感受算法思想的基础上,结合对具体数学实例的分析,体验程序框图在解决问题中的作用;通过模仿、操作、探索,学习设计程序框图表达解决问题的过程;体会算法的基本思想以及算法的重要性和有效性,发展有条理的思考与表达的能力,提高逻辑思维能力。
(一)内容要求
高中数学《课程标准》将算法编排在必修模块的数学3中。其内容和要求如下:
1.算法的含义、程序框图
(1)通过对解决具体问题过程与步骤的分析(如,二元一次方程组求解等问题),体会算法的思想,了解算法的含义。
(2)通过模仿、操作、探索,经历通过设计程序框图表达解决问题的过程。在具体问题的解决过程中(如,三元一次方程组求解等问题),理解程序框图的三种基本逻辑结构:顺序、条件分支、循环。
2.基本算法语句
经历将具体问题的程序框图转化为程序语句的过程,理解几种基本算法语句--输入语句、输出语句、赋值语句、条件语句、循环语句,进一步体会算法的基本思想。
3.通过阅读中国古代数学中的算法案例,体会中国古代数学对世界数学发展的贡献。
另外,《新课程标准》还要求把算法思想渗透在其他相关内容之中,中学数学中的算法内容和其他内容是密切联系在一起的,比如线性方程组的求解、数列的求和等。
(二)设置算法内容的依据
在现代社会里,计算机已经成为人们日常生活和工作不可缺少的工具。计算机几乎可以是一个全能的助手,你可以用它来做你想做的任何事情。“算法过程”即是机械式地按照某种确定的步骤行事,通过一系列小的简单计算操作完成复杂计算的过程。人类最早关于算法的纪录存在于在两河流域发现的公元前两三千年的泥板书上,其中的一个典型例子就是计算利息何时能够等于本金。算法早期发展中值得一提的另一个成果应归功于古希腊的欧几里得,他提出的计算最大公约数的辗转相除法(又称欧几里得算法)至今仍在使用。中国古代数学研究中也有许多有关算法的成果。用我国传统的开方术求高次方程的近似根,是算法上的一大成就。
现代意义上的“算法”通常是指可以用计算机来解决的某一类问题的程序或步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成。比如,我们非常熟悉的带余除法、线性方程组的消元法等,都是算法。
算法和计算机有着密切的联系,计算机解决任何问题都要依赖于算法。只有将解决问题的过程分解为若干明确的步骤,即算法,并用计算机能够接受的“语言”准确的描述出来,计算机才能解决问题。因此,算法是计算机科学的重要基础,没有算法也就没有计算机。
(三)算法内容的引入的重要教育价值
算法内容的引入有其重要的教育价值,主要体现在以下几个方面:
1.有利于培养学生的思维能力
算法一方面具有具体化、程序化、机械化的特点,同时又有抽象性、概括性和精确性。对于一个具体算法而言,从算法分析到算法语言的实现,任何一个疏漏或错误都将导致算法的失败。因此,培养逻辑思维能力,不仅可以通过几何论证、代数运算等手段来进行,还可以通过算法设计的学习来达到。
2.有利于培养学生理性思维和实践能力
算法既注重“算则”,更注重“算理”,对于算法而言,一步一步地程序化步骤,即“算则”固然重要,但这些步骤的依据,即“算理”有着更基本的作用。“算法”是“算则”的基础,“算则”是“算理”表现。算法思想可以贯穿于整个中学数学内容之中,有很丰富的层次递进的素材,而在算法的具体实现上又可以和信息技术相联系,因而,算法有利于培养学生理性思维和实践能力,是实施探究性学习的良好素材。
3.有利于学生理解构造性数学
构造性地解决数学问题不仅是重要的解决数学问题的方法,在数学哲学上也有重要的意义。构造性数学是一个重要的数学哲学学派,他们只承认构造出来的数学,这种观念有其特定的真理性。
4.算法内容反映了时代的特点,同时也是中国数学课程内容的新特色
中国古代数学以算法为主要特征,取得了举世公认的伟大成就。现代信息技术的发展也使算法焕发了前所未有的生机和活力,算法进入中学数学课程,既反映了时代的要求,也是中国古代数学思想在一个新的层次上的复兴,成为中国数学课程的一个新特色。
算法思想在高中数学课程中主要是以分散、渗透的方式进行呈现的。《新课程标准》力求把算法融入到数学课程的各个相关内容当中,中学数学中有很多内容是和算法内容密切联系在一起的。一般情况下,能够利用概念、公式或者定理、法则来解题的过程都可以看成算法的过程,都可以用程序框图或程序语言来描述。《新课程标准》要求在教学中应注意挖掘教材,合理选择相关内容渗透算法。在其它内容中渗透算法的目的有两个:一方面借助直观的算法表示(比如程序框图),有利于学生更好地理解该内容;另一方面也有利于学生进一步学习算法,体会算法思想。
能够和算法结合的内容有很多,比如线性方程组的解法,求一元二次方程的根,还有函数奇偶性、单调性的判定,数列求和,随机试验模拟等等。以下提供几个案例:
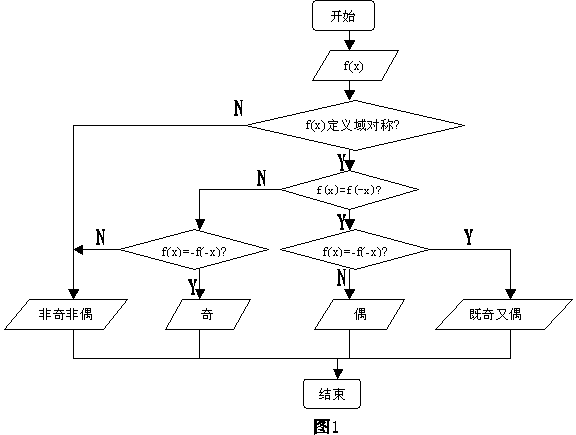
例1 用算法程序框图描述判断一个函数奇偶性的步骤。
算法分析:
第一步:判断f(x)定义域是否对称,若否则f(x)非奇非偶,若是则执行第二步;
第二步:计算f(-x),判断f(-x)与f(x)的关系,若f(-x) =f(x)①,则f(x)是偶函数;若f(-x) =-f(x)②则f(x)是奇函数;若①②都成立,则f(x)是既奇又偶函数;若①②都不成立,则f(x)是非奇非偶函数。
程序框图如图1所示。
例2 小明要登上一个20级的台阶,如果他每次只能登上一级或两级台阶,问登上台阶一共有多少种方法?
分析:采用倒推法。假设登上20级台阶的方法数计为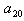 ,小明迈完一步以后他面临两种情况:若他第一步登了1级,还剩余19级,可能方法数为 ,小明迈完一步以后他面临两种情况:若他第一步登了1级,还剩余19级,可能方法数为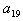 ;若他第一步登了2级,还剩余18级,可能的方法数 ;若他第一步登了2级,还剩余18级,可能的方法数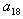 。根据加法原理, 。根据加法原理,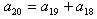 ,类推到一般情形有 ,类推到一般情形有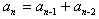 (n>2).由于 (n>2).由于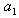 =1, =1,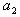 =2,故可推出 =2,故可推出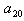 。 。
程序框图如图2,写成程序如下:
input“n=”;n
p=1
q=2
i=3
do while i<=n
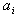 =p+q =p+q
p=q
q=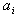
i=i+1
loop
print“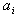 =”; =”;
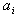
end |
 |
运行程序时,只要输入n=20即可得出本题结果。此程序还可以用于解当n取其它值时情形。由结果可以看出在{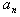 }前再添加一项“1”,该数列则变成斐波那契数列,所以该题其实是斐波那契数列的应用。 }前再添加一项“1”,该数列则变成斐波那契数列,所以该题其实是斐波那契数列的应用。
例3 编程序,模拟随机试验:多次投硬币,求出现正面的频率。
分析:利用RND函数产生(0,1)之间随机数,再利用INT(RND(1)*2),便可随机产生0,1两个数。以0代表出现反面,1代表出现正面。程序如下:
input“n=”;n
z=0
for i=1 to n
t=int(rnd(1)*2)
if t=1 then
z=z+1
end if
next i
print“z=”;z
print“p=”;z/n
利用该程序,只需输入循环次数n(就好比投掷硬币的次数),就能输出出现t=1的次数z(就好比出现正面的次数),以及频率p。
另外,在选修3-1《数学史选讲》专题中也可以渗透算法思想。《标准》对该部分提供了几个可供选择的选题,其中涉及中国古代数学的选题多与算法有关,比如,“早期的算术与几何——计数与测量”,“中国古代数学瑰宝”,“算法思想的历程”等。
《新课程标准》对算法部分的内容进行了如下说明与建议:
1.算法是高中数学课程中的新内容,其思想是非常重要的,但并不神秘。例如,运用消元法解二元一次方程组、求最大公因数等的过程就是算法。本模块中的算法内容是将数学中的算法与计算机技术建立联系,形式化地表示算法,在条件允许的学校,使其能在计算机上实现。为了有条理地、清晰地表达算法,往往需要将解决问题的过程整理成程序框图;为了能在计算机上实现,还需要将自然语言或程序框图翻译成计算机语言。本模块的主要目的是使学生体会算法的思想,提高逻辑思维能力。不要将此部分内容简单处理成程序语言的学习和程序设计。
2.算法教学必须通过实例进行,使学生在解决具体问题的过程中学习一些基本逻辑结构和语句。有条件的学校,应鼓励学生尽可能上机尝试。
3.算法除作为本模块的内容之外,其思想方法应渗透在高中数学课程其他有关内容中,鼓励学生尽可能地运用算法解决相关问题。
在教学过程中,对算法内容,应着重强调使学生体会算法思想、提高逻辑思维能力,不应将算法简单处理成程序语言的学习和程序设计,同时应通过具体实例的上机实现(或编程)帮助学生理解算法思想及其作用。标准对传统内容的编排和要求也有新的变化,为了更好地理解和把握,有效地进行教学,教师应进行必要的探索和研究,提高自身的数学专业素质和教育科学素质。
|

