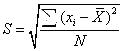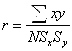五、数学教育评价中的常用统计量和统计方法

    教育统计是统计的原理和方法在教育科学研究中的具体应用。统计方法是通过观测、调查和实验对所收集到的数据资料进行整理、计算、分析解释和统计检验的原理和方法，是数学教育评价的重要工具和方法，是达到定量化地进行数学教育评价的有力手段。
    统计方法主要是对数据资料的科学处理。在数学教育评价中，乃至一般的数学教育科学研究中，运用统计方法对数据进行科学处理从而做出定量分析，是数学教育评价（包括数学教育研究）的发展趋势。我们在这里简单扼要的介绍一下在数学教育评价中常用的一些统计量和统计方法。

    （一）总体和样本

    把一个研究所指向对象的集合的全体当作统计研究对象时，就叫做总体。例如，要研究初中一年级学生的数学能力发展水平，那么所有的初中一年级学生就是总体。但是由于受客观条件的限制，往往不可能对所有的对象（总体）进行研究，而总是抽取其中典型的一部分进行研究。这种从总体中取出部分个体的过程叫做“抽样”，所抽得的部分成为样本。例如，在上例中如果选择好、中、差三所学校进行测查，那么这三所学校的初中一年级学生就是样本。一般来说，数学教育评价（研究）中，往往是用样本来代表总体，即依据样本所得到的结果，来推断总体的结果。所以抽取样本时要注意典型性。

    （二）集中量数

    集中量数就是代表数据分布集中趋势的量数。表示集中量数的有：算术平均数、加权平均数、中数、众数和几何平均数。

    1．算术平均数也称平均数或均数。一般用表示算术平均数。若设变量…，代表各个变量的观察值为观察总次数，则计算的公式为：
    算术平均数能从总体上评价两组变量的情况。例如，评价两个班的数学学习情况，可用两个班的数学学习成绩的平均值来进行。甲班平均分为85分，乙班平均值为91分，那么在一定意义上可以表明乙班学习的数学学习优于甲班。
    算术平均数是将各变量的重要性同等看待，但实际上，有时各变量的重要性是不同的，这是一般采用“加权”的办法。加权平均数是把各变量所代表的观察值分别乘以权数之和。若设分别为的权数，那么

    例如，数学期中考试和期末考试对学生的数学总成绩的贡献就是有权重的，一般来说期末考试占70%，期中占30%，那么前者的权重就是0.7，后者的权重是0.3。若某学生期中是90分，期末是80分，那么其加权平均数就是。
    算术平均数反应灵敏，计算简便，较少受抽样变动的影响。但当数据性质不同或者包含有极端数据是，应避免采用算术平均数作为集中趋势的指标。
    2．中数，又称中位数，它是位于一组数据中较大一半与较小一半中间位置的数。中数可能是原始数据中的一个，也可能并不是原有数据。中数计算简便，但反应不够灵敏，对于极端数据不如算术平均数敏感，中数受抽样的影响较大，稳定性不如算术平均数。因此，通常中数不被普遍使用。
    3．众数，是指一组数据中出现次数最多的某个数据值。众数可通过观察的方法直接得到，也可用积分的方法求出。众数不够稳定，易受样本变动的影响，但较少受极端数据的影响，反应不灵敏。在要求粗略的快速计算中，计算简便。一般不常用。

    （三）差异量数

    描述一个分布时，有时采用集中量数还不能够看出两组变量的全貌，这就要研究差异量数。差异量数是表示一组数据的差异情况或离散程度的量数。应用最广的是标准差，用字母表示，其公式是：
    其中，表示各变量的观察值（如各学生的成绩分数）；表示平均数；为总次数（如班级人数）。
    如果我们求得一个年级男生数学成绩的标准差，女生的标准差，从标准差可以看出，男生数学成绩的离散程度大于女生，说明有的男生成绩偏高，有的偏低，不像女生那样保持着整体的一致。

    （四）相关性

    相关性是指两组变量的相互关系。例如，智力与学习成绩的关系；数学成绩与数学能力发展的相互关系等。
    相关分为正相关、负相关和零相关三种。若两组变量的变动方向相同，即一组变量变化时，另一组变量也产生相应的变化，这两组变量的关系叫正相关，否则叫负相关。零相关表示没有关系。
    相关程度如何，一般用相关系数来表示（用字母表示）。相关系数的计算公式为：
    其中，；；为成对的变量数目，为变量的标准差；为变量的标准差。
    相关系数在数学教育评价中应用十分广泛，相关的程度可以根据相关系数查相关显著性表来确定，例如，求得了学生数学成绩和学生数学概括能力测试成绩的相关系数为0.336，查相关显著性表，在次数44时的临界值为0.291，这说明学生数学成绩和数学概括能力发展呈显著相关。

    （五）差异显著性检验

    在数学教育评价中，有时除了用上面介绍的量来刻画以外，还要考察显著性是否有意义。差异显著性检验一般用-检验、-检验、-检验和-检验。这在一般的教育统计书上都有详细介绍，这里就不再做具体介绍了。
    统计方法根据其内容和方法的不同，可分为描述统计和推断统计。描述统计是将收集来的大量数据资料，加以整理、归纳和分组，简缩成易于处理和便于理解的形式，并计算所得数据的各种统计量，如平均数、标准差、相关系数等，以此来描述有关事物或现象的分布情况、波动范围和相关程度等，以揭示其特点和规律。推断统计是在描述统计的基础上的，用抽样的方法从对样本的研究中所得的统计量来推断总体的有关特征，以便做出具体的计划和决策。